Seguramente te haya llegado a los oídos algo sobre interés compuesto, pero desconozcas su uso y cómo se calcula.
La fórmula del interés compuesto es (1+i)^n, donde i es el tipo de interés y n el número de periodos. Para capitalizar un capital hay que multiplicar esa fórmula al capital invertido, C_0*(1+i)^n, y para actualizarlo hay que dividir el capital futuro por la fórmula, \frac{C_f}{(1+i)^n}.
Quédate hasta el final porque te voy a contar cómo vas a poder usar la fórmula del interés compuesto para mover capitales en el tiempo, cómo calcularlo en Excel y qué hacer si el tipo de interés no es anual.
Fórmula del interés compuesto
Como te revelaba al principio, la fórmula del interés compuesto es la siguiente, (1+i)^n.
Esta fórmula se usa para calcular el valor de ciertos capitales en diferentes momentos del tiempo.
Por ejemplo, imagina que tienes unos ahorros y quieres saber cuánto dinero tendrás si lo inviertes a un tanto de interés dentro de 15 años. O, por el contrario, dentro de 10 años quieres tener 10.000€ y quieres saber cuánto tienes que invertir hoy, o incluso a qué tasa tienes que invertir el dinero que tienes.
Este es un uso personal, pero te lo cuento para que lo entiendas, aunque el uso del interés compuesto se extiende a otros conceptos más amplios como a las finanzas empresariales para el cálculo de viabilidad de proyectos, y otros ámbitos privados como préstamos, tarjetas de crédito, hipotecas, …
Para saber de dónde sale la fórmula, hay que entender dos cosas primero:
- La particularidad del interés compuesto es que los intereses se reinvierten.
- Capitalizar consiste en llevar capitales actuales al futuro y actualizar lo contrario, del futuro al presente.
Una vez entendidos estos dos matices, ya podemos comprobar de dónde sale la fórmula del interés compuesto.
Capitalización compuesta
Para conocer de dónde nace la fórmula, conviene hacerlo con la capitalización, es decir, tienes un dinero y quieres saber cuánto tendrás dentro de X años. Acuérdate que con interés compuesto los intereses se reinvierten.
Vamos paso a paso.
En el momento actual tienes un dinero, o capital inicial, C_0, digamos 10.000€.
La inversión es al 10%, por tanto, al año, o periodo siguiente, C_1, cobras los intereses, que al ser del 10% sobre 10.000€, son de 1.000€, obteniendo un total de 11.000€, y esto se expresa así,
C_1=10.000+10.000*10\%=10.000*(1+10\%)
Si se expresa en modo formal,
C_1=C_0+C_0*i=C_0*(1+i)
En el segundo año o periodo, se perciben intereses del total, es decir, capital invertidos más los intereses generados anteriormente.
En este caso, obtenemos otros 1.000€ del capital inicial, y 100€ de los 1.000€ de intereses anteriores; que es lo mismo que percibir 1.100€ de los 11.000€ que se tienen en el momento 1.
C_2=11.000+11.000*10\%=11.000*(1+10\%)=12.100€\\ C_2=C_1*(1+i)=C_0*(1+i)*(1+i)=C_0*(1+i)^2
Podríamos seguir así hasta el infinito (y más allá), pero creo que has pillado el concepto, así que, si quieres capitalizar cualquier capital a cualquier momento futuro, debes aplicar la siguiente fórmula que nace de la explicación anterior,
C_n=C_0*(1+i)^n
Tan solo debes sustituir los valores que tengas en la fórmula para realizar el cálculo, veamos algún ejemplo:
- Has recibido un dinero (herencia, lotería, regalo, …), 25.000€, que quieres invertir para tu jubilación dentro de 30 años y la rentabilidad esperada es del 3,5%, por tanto, dentro de 30 años tendrías, C_{30}=25.000*(1+3,5\%)^30=70.169,84€.
- Al nacer tu hijo has juntado unos ahorros y un dinero que te han dado tus familiares, 13.000€, y los has metido en un fondo que tiene una rentabilidad anual media del 7,8% con la intención de que al cumplir su mayoría de edad disponga de un dinero, C_{18}=13.000*(1+7,8\%)^18=50.243,63€.
Estos han sido solo algunos de los ejemplos, lo que más me gusta es crear escenarios posibles y ver las capacidades financieras de cada individuo o proyecto, ahora te toca a ti evaluar tus finanzas.
Por cierto, en este otro artículo te cuento cómo calcular el capital final en interés compuesto al detalle.
Actualización compuesta
Aquí tenemos que pensar al revés, siguiendo el ejemplo anterior, si quiero que mi hijo tenga 50.000€ cuando cumpla la mayoría de edad, ¿cuánto dinero tengo que invertir hoy?
Y es que la palabra lo dice, actualizar capitales del futuro al presente, con interés compuesto.
Para mostrarte la fórmula podría pasar por el mismo proceso de antes, pero vamos a tomar un atajo puesto que ya has entendido de donde viene la fórmula del interés compuesto.
Lo único que debemos hacer es despejar de la fórmula anterior el único factor que desconocemos, que es el capital actual, C_0, tal que,
C_n=C_0*(1+i)^n \rightarrow C_0=\frac{C_n}{(1+i)^n}=C_n*(1+i)^{-n}Listo, ahora solo hay que cambiar los números para ver qué obtenemos y realizar los cálculos que necesitemos.
Siguiendo los ejemplos anteriores:
- Si para la jubilación te gustaría tener 70.000€ dentro de 30 años y con una rentabilidad esperada del 3,5%, ahora necesitas invertir, C_0=70.000*(1+3,5\%)^{-30}=24.939,49€.
- En el caso de que tu hijo necesite 50.000€ para su mayoría de edad y el fondo arroje una rentabilidad del 7,8%, C_0=50.000*(1+7,8\%)^{-18}=12.936,96€.
Como ves, una vez sabes la fórmula de capitalización compuesta y el término del interés compuesto ya puedes encontrar cualquier elemento que te falte, tan solo debes sustituir en la ecuación, o aplicar las fórmulas que te dejo.
La Fórmula del interés compuesto en Excel
Hacer estos cálculos, cuando tienes que hacer muchos, es tedioso y puede que no te aclares mucho, aunque con la calculadora de tu teléfono móvil es suficiente.
Así que te voy a mostrar cómo configurar paso a paso una hoja de Excel para realizar en cuestión de minutos muchísimos cálculos de forma casi inmediata. (Y también te dejaré la hoja).
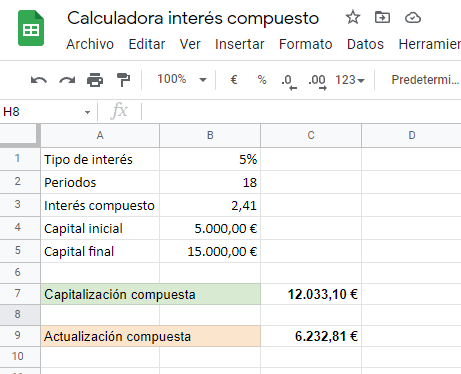
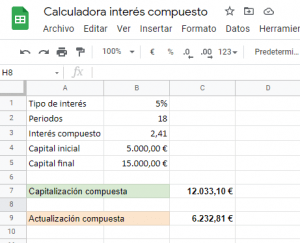
Aquí se pueden ver todos los datos. El tipo de interés, periodos, y capital inicial y final, son datos que deberás introducir tú, dependiendo de qué quieras calcular.
Luego, las casillas de interés compuesto, capitalización y actualización ya están configuradas para que cuando cambies el resto de casillas anteriores te salgan los cálculos de forma inmediata.
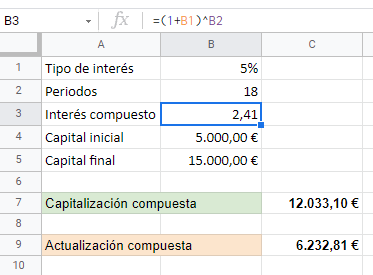
La casilla de interés compuesto muestra el factor multiplicador, es decir, la primera fórmula que escribí en la introducción, (1+i)^n. Como ves, lo único que hacemos es pasar lo del papel al ordenador.
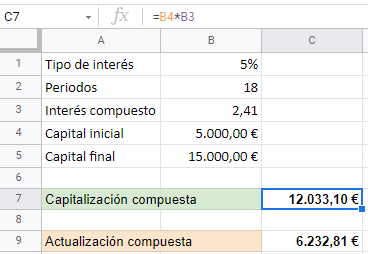
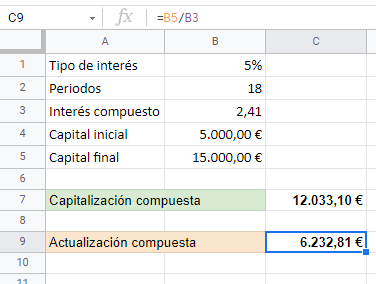
Ahora, las casillas de capitalización y actualización lo único que hacen es multiplicar o dividir el capital necesario entre el interés compuesto.
En el caso de la capitalización se multiplica el capital inicial, C_0*(1+i)^n; mientras que en la actualización se divide, \frac{C_n}{(1+i)^n}. Esto es todo.
Aquí te dejo la hoja de Excel para que la puedas descargar y usar, ya que como podrás comprobar en cuanto hagas algún cambio se actualiza al ejemplo que quieras calcular.
Calculadora de interés compuesto
Otra forma de realizar estos cálculos es buscar una calculadora de interés compuesto en internet y seguro que te saldrán algunas que te permitirán hacer lo mismo que te he mostrado antes.
Mi amigo Marc tiene una calculadora que es bastante útil.
También puedes descargar el Excel anterior que te servirá y siempre lo tendrás guardado en tu dispositivo.
Así es cómo se ve la calculadora de Marc de Opinatrón

¿Cómo calcular el interés compuesto diario?
Hasta ahora te he mostrado cómo calcular el interés compuesto en general y cómo usarlo tanto para capitalizar, como para actualizar, pero, ¿qué pasa si el tipo de interés no es anual?
El concepto clave aquí para hacer el cálculo con el tipo de interés compuesto diario es entender que, al finalizar el año, el resultado de la capitalización debe ser igual, no importa el periodo del tipo de interés.
Si recopilamos, la capitalización compuesta anual es C_n=C_0*(1+i)^n, haciendo una pequeña transformación obtenemos cómo debe ser el capital al cabo de un año si el interés es diario.
C_{365}=C_0*(1+i_{365})^{365}Hemos introducido el interés diario, i_{365}, y se ha elevado a 365, que son los días que tiene un año para saber el capital final en un año.
Para encontrar el tipo de interés compuesto diario, sabemos que el capital final debe ser igual no importa cuál sea la periodicidad del tipo de interés, así que lo que hacemos es igualar los capitales finales (diario y anual):
C_0*(1+i)^1=C_0*(1+i_{365})^{365}Como el capital inicial es el mismo, no es relevante y se puede eliminar de la ecuación, y solo quedaría despejar el interés diario, de tal modo que,
i_{365}=(1+i)^{\frac{1}{365}}-1Del mismo modo, si tenemos el interés compuesto diario y lo queremos pasar a anual, pues tendremos que despejarlo,
i=(1+i_{365})^{365}-1Como ejemplo, si el tipo de interés anual es del 7,8%, el diario será de i_{365}=(1+7,8\%)^{\frac{1}{365}}-1=0,02058\%.
De igual modo, si el tipo de interés diario es del 0,25%, el anual será i=(1+0,25\%)^{365}-1=148,77\%.
Aquí te dejo una tabla a modo resumen para que puedas practicar con la calculadora:
| Anual | Diario |
| 5.00% | 0.01337% |
| 10.00% | 0.02612% |
| 25.00% | 0.06115% |
| 50.00% | 0.11115% |
Otros periodos diferente al diario
Si quieres otros periodos diferente al diario, es muy sencillo, con una pequeña transformación de la fórmula anterior se consigue.
i_{k}=(1+i)^{\frac{1}{k}}-1Donde k es el número de periodos que tiene en un mismo año.
Por ejemplo, en diario es igual a 365, pero en semestral k=2, trimestral k=4, semanal k=52, … entiendes el concepto, ¿verdad?
Tan simple y tan sencillo como esto, aunque si quieres más detalle, en este otro artículo te cuento cómo calcular otros periodos diferente a un año como el mensual o el semestral.
Puntos clave
El interés compuesto se usa en casi todos los productos financieros y, de un modo u otro forma parte de nuestras vidas, aunque no lo sepamos.
De ahí radica la importancia a conocerlo y saber cómo usarlo, y estos son los puntos clave del artículo.
- La fórmula del interés compuesto nos sirve para mover capitales en el tiempo y hacer planificación financiera, así como evaluar proyectos de inversión.
- La particularidad del interés compuesto es que los intereses se reinvierten, aspecto que sucede en la mayoría de productos financieros.
- Se puede adaptar el cálculo a cualquier periodo de tiempo, lo que nos dota de flexibilidad.
Espero que hayas entendido bien cuál es la fórmula del interés compuesto y cómo sacarle partido, cualquier duda o pregunta no dudes dejarla en los comentarios.


Gracias. Muy clara la explicación.
Quizá podría incluirse la explicación del cálculo con tasa variable y aportaciones variables.
Un saludo