En este artículo, discutiremos cómo resolver problemas matemáticos de interés simple.
El interés simple es el concepto de calcular una cantidad de dinero ganada o pagada durante un período de tiempo específico, y se usa a menudo cuando se habla de pagos de préstamos y ganancias de inversiones.
Veremos una descripción general del proceso de cálculo, así como consejos y trucos para ayudarte a comprender las matemáticas detrás del interés simple.
Resolver problemas de interés simple
En este artículo vamos a resolver los problemas del interés simple, cualquier aspecto que se puede calcular con matemáticas sencillas, ya que como dice el interés, es simple.
Para ello debemos atender a los elementos que componen el interés simple, para ver más tarde con un ejemplo qué podemos calcular y cómo hacerlo.
Los elementos del interés simple son los siguientes:
- El capital a invertir o principal
- El tipo de interés o rentabilidad de la operación
- El número de veces o periodos que vamos a realizar la inversión
- El capital final o resultado que voy a obtener
Todos estos elementos están presentes en la fórmula del interés simple, y si quieres ver un análisis más exhaustivo de cada uno de los factores visita el siguiente artículo.
Usando la fórmula del interés simple
Antes de escribir ninguna fórmula hay que entender dos términos: capitalizar y actualizar.
Capitalizar consiste en coger un capital a día de hoy, una inversión, y hacerlo crecer a lo largo del tiempo. En definitiva, el concepto de invertir.
Mientras que actualizar, consiste en hacer lo contrario, es decir, si dentro de 10 años quiero tener 15.000 €, ¿cuánto tengo que invertir hoy? La actualización se utiliza para evaluar inversiones.
Vamos a plasmar la fórmula de capitalización simple, que consiste en hacer un capital a lo largo del tiempo si invertimos con interés simple.
La fórmula es la siguiente:
C_f=C_0 · (1+r·n)
Esta fórmula responde a cuánto dinero voy a obtener, C_f , si invierto un capital a día de hoy, o principal, C_0 , a una tasa de interés fija, r , durante 20 años, n .
Trabajar a través de un ejemplo
Vamos a suponer un ejemplo sencillo donde una persona va a invertir 5.000 € durante 20 años a una tasa de interés fija del 5 %.
Si quieres conocer las matemáticas que están debajo de este ejemplo, te recomiendo que leas este otro artículo donde te cuento cómo obtener cada fórmula que presento a continuación.
Cálculo del capital final con interés compuesto
Para realizar el cálculo, tan solo hay que sustituir los datos en la fórmula anterior de capitalización compuesta:
C_f=C_0 · (1+r·n)=5.000 · (1+0,05·20)=10.000 €
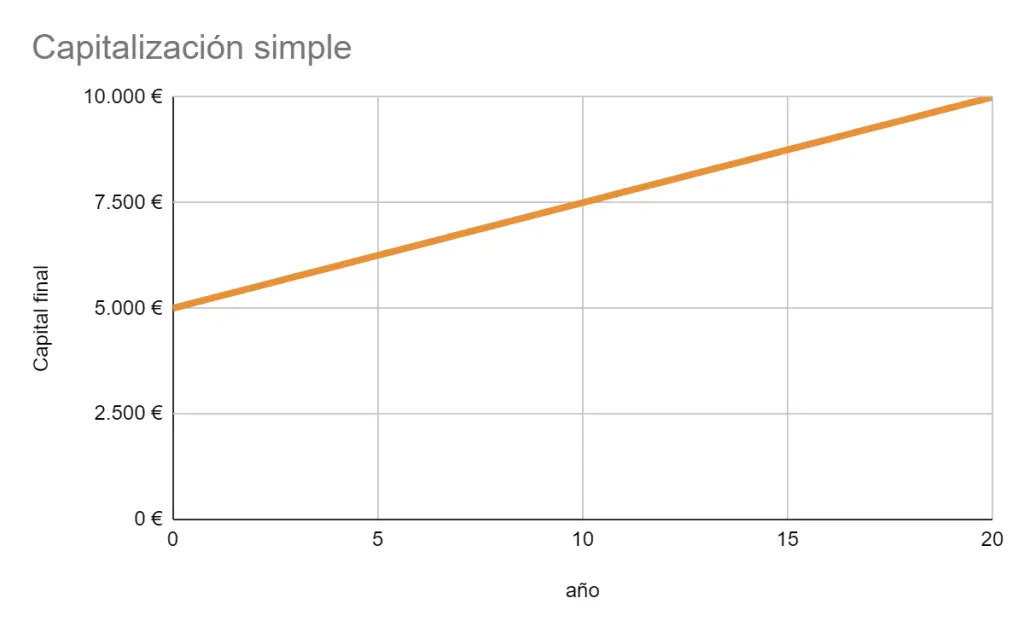
Cuando se capitaliza capital con interés simple, cada año se invierte la misma cantidad, es decir, los 5.000 €, que como el tipo de interés es del 5 %, se obtienen unos intereses de 250 € al año.
Gráficamente se observa cómo el crecimiento es lineal:
Cálculo del principal con interés simple
En este caso, buscamos conocer cuánto tenemos que invertir si queremos logar un capital en concreto, es decir, actualización con interés simple.
Siguiendo el ejemplo, imagina que quieres lograr 15.000 € dentro de 20 años invertidos al 5% anual. ¿Cuánto dinero tienes que invertir?
Para ello, debemos transformar la fórmula de modo que la fórmula de actualización simple es la siguiente:
C_0=\frac{C_f}{1+r·n}=\frac{15.000}{1+0,05·20}=7.500 €Se necesitan invertir 7.500 € a día de hoy para tener 15.000 € dentro de 20 años.
| Año | Capital inicial |
| 0 | 15.000 € |
| 1 | 14.286 € |
| 2 | 13.636 € |
| 3 | 13.043 € |
| 4 | 12.500 € |
| 5 | 12.000 € |
| 6 | 11.538 € |
| 7 | 11.111 € |
| 8 | 10.714 € |
| 9 | 10.345 € |
| 10 | 10.000 € |
| 11 | 9.677 € |
| 12 | 9.375 € |
| 13 | 9.091 € |
| 14 | 8.824 € |
| 15 | 8.571 € |
| 16 | 8.333 € |
| 17 | 8.108 € |
| 18 | 7.895 € |
| 19 | 7.692 € |
| 20 | 7.500 € |
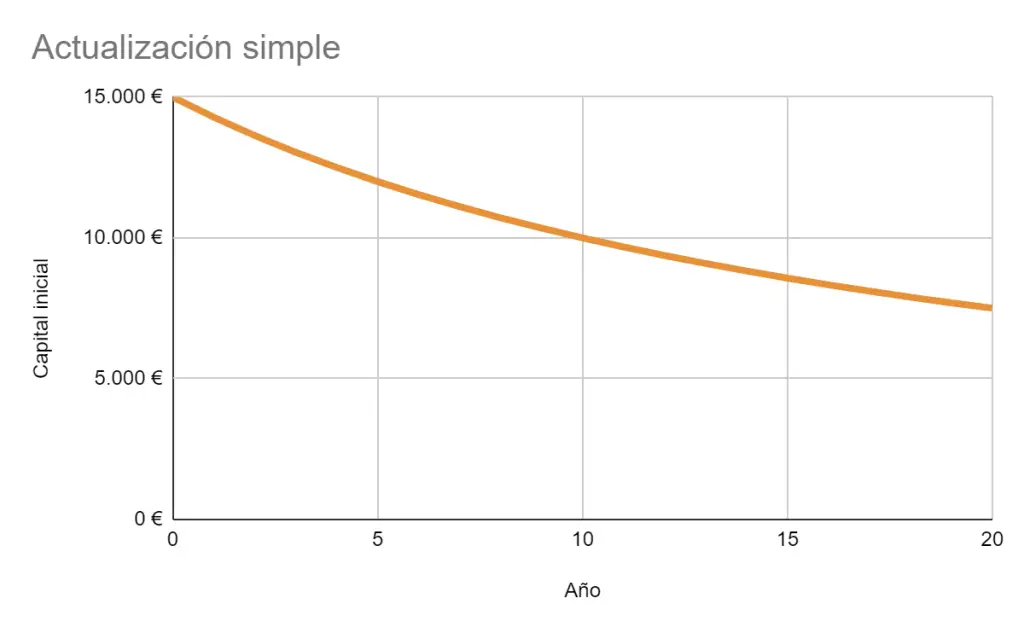
Arriba aparece una tabla que muestra cuánto dinero se necesita invertir para lograr 15.000 € dependiendo el número de años que se vaya a invertir.
Cálculo de la tasa de interés
Volviendo al ejemplo inicial, imagina que necesitas 15.000 € dentro de 15 años, y ahora mismo solo tienes 5.000 € para invertir, entonces, ¿qué tipo de interés debes lograr?
En este caso, te da una pista para que puedas evaluar los diferentes instrumentos financieros y decidir dónde invertir.
Para conocer esa tasa de interés, hay que volver a trabajar sobre la fórmula del interés simple para despejar el tipo de interés, de modo que:
r=\frac{\frac{C_f}{C_0}-1}{n}=\frac{\frac{15.000}{5.000}-1}{15}=13,33\%Para logra tus objetivos con tu situación actual debes lograr un vehículo de inversión que te aporte una rentabilidad anual del 13,33 %.
Cálculo del período de tiempo con interés simple
Por último, nos queda evaluar cuanto tiempo necesitamos para lograr nuestros objetivos.
Imagina que quieres lograr con un capital de 5.000 €, 15.000 € invertidos al 5 %, entonces, ¿cuánto tiempo te va a llevar lograrlo?
Como antes, hay que trabajar sobre la fórmula de la capitalización simple para despejar el tiempo y poder resolver los problemas.
n=\frac{\frac{C_f}{C_0}-1}{r}=\frac{\frac{15.000}{5.000}-1}{0,05}=40En este caso, se necesitan 40 años para triplicar el capital, quizás sea demasiado, así que puedes jugar con la rentabilidad o el capital invertido para acortar la duración.
Conclusión: Dominar los problemas de interés simple
En conclusión, la resolución de problemas matemáticos de interés simple es una habilidad muy útil que todo el mundo debería tener.
Con la ayuda de este artículo, ahora conoces las fórmulas básicas que debes usar para resolver problemas de interés simple. También entiende cómo encontrar la tasa, el tiempo, el capital o el interés usando las fórmulas dadas.
Por último, con estas herramientas en la mano, debería poder abordar cualquier problema relacionado con el interés simple con confianza y precisión.