Al enfrentarse a cualquier inversión, bien sea privada o empresarial, algo que queremos conocer, aunque a veces es desconocido, es la rentabilidadz, es decir, cuánto vamos a ganar.
Para calcular la tasa interna de retorno (TIR) se ha de igualar el valor actual neto (VAN) de todos los flujos de un proyecto a cero, y computar el valor de la tasa de descuento o rentabilidad. Dependiendo de cómo de complejo sea el VAN, así será la dificultad del cálculo.
A continuación, voy a mostrarte cómo calcular el TIR a mano tanto si la fórmula del VAN es de primer, segundo o mayor grado, además del cálculo con hoja de cálculo, Excel y Google Sheets.
Cómo calcular la tasa interna de retorno manualmente
Antes de entrar en materia, y si es de tu interés, en este otro artículo te cuento qué es la TIR y sus principales ventajas y desventajas.
Da igual el modo en que la calcules, la TIR es la tasa que hace el VAN cero, de tal modo que:
VAN=\sum_{i=0}^n\frac{F_i}{(1+TIR)^i}=0donde la F representa a los diferentes flujos de caja en los diversos periodos de tiempo.
Los flujos de caja pueden ser positivos o negativos, es más, en la realidad habrá flujos de todo tipo, y el hecho de que haya flujos negativos no afecta al cálculo de la TIR, sino que se integran igual que el resto.
Eso sí, en ese caso en vez de sumar al VAN, restarán, es decir, el signo dependerá de cómo sea el flujo. Con esta breve explicación ya sabrás cómo calcular la TIR con flujos negativos.
Voy a calcular la TIR aumentando su nivel de dificultad para que aprendas a aplicar la forma correcta dependiendo de tu caso.
Calcular la TIR a un periodo
Imagina la inversión de 1.000€ a un año, donde se recibe un pago final de 1.500€, matemáticamente se expresa como:
VAN=-1.000€+\frac{1.500€}{1+TIR}=0Este es el caso más sencillo, así que si despejamos la TIR:
TIR=\frac{1.500€}{1.000€}-1=0,5Se observa que la tasa interna de retorno es de un 0,5 que expresado en porcentaje es de un 50%, es decir, en un año se obtiene un 50% de rentabilidad sobre el capital invertido.
Pero, ¿qué pasa si son dos periodos?
Calcular la TIR en dos periodos
Igual que antes, tenemos una inversión de 1.000€ con un flujo de 750€ en los dos años posteriores, tal que:
VAN=-1.000€+\frac{750€}{1+TIR}+\frac{750€}{(1+TIR)^2}=0En este caso, se recupera la misma cantidad de 1.500€, pero en el doble de tiempo.
Pero ahora despejar la TIR se hace más complicado, por tanto debemos usar otra metodología.
Como se puede observar se tienen un polinomio de grado dos, por lo que podemos usar la fórmula de ese polinomio haciendo una pequeña transformación.
En este caso entendemos que,
X=\frac{1}{1+TIR}De modo que el polinomio de grado 2 es:
750 X^2+750 X-1.000=0
y se debe resolver que:
X= \frac {-b \pm \sqrt {b^2 - 4ac}}{2a}donde, a es el término al cuadrado (el primer 750), b el término de X (el otro 750) y c es -1.000.
Al resolver se obtienen dos valores, de los cuales uno es negativo y por tanto se descarta, así que solo voy a escribir el primero que nos dice que X=0,7583, así que ahora solo queda obtener la TIR.
TIR=\frac{1}{X}-1=0,3187En este caso, la TIR es de casi un 32%, cifra menor que en el anterior caso puesto que se consigue el resultado en el doble de tiempo, y era algo a esperar.
¿Y si son más de dos periodos?
En este caso no se puede resolver de manera directa a menos que se haga una aproximación a través del método de semejanza de triángulos por aproximación.
Siguiendo con el ejemplo anterior, ahora tenemos tres pagos, el primer año de 450€, el segundo de 500€ y el tercero de 550€.
Al obtener la misma cantidad en un año más, sabemos que la rentabilidad anual va a ser menor, porque no es lo mismo conseguir 500€ en uno, dos o tres años, ¿verdad?
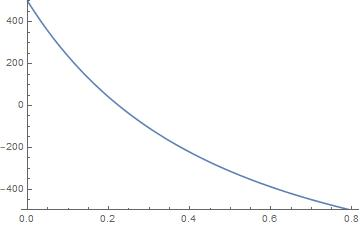
Este es el gráfico que representa la relación TIR-VAN, donde el eje de las x, el horizontal representa el TIR, mientras que el de las y, vertical, el VAN.
Al ser una curva, se hace una aproximación lineal a través de un triángulo que hace que el cálculo sea muy simple, aunque no deje de ser una aproximación bastante certera.
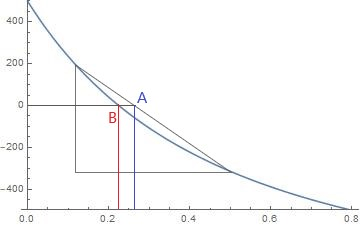
En este caso, vemos como esa aproximación lineal está representada por el triángulo y el TIR calculado es el que marca el punto A, que es siempre mayor que el TIR real que es el del punto B.
Ahora es cuando entra en juego la ley de semejanza de triángulos, que indica que todos los triángulos rectángulos son proporcionales, entonces sabiendo la proporcionalidad de un triángulo se puede extrapolar al resto para conocer esa TIR aproximada.
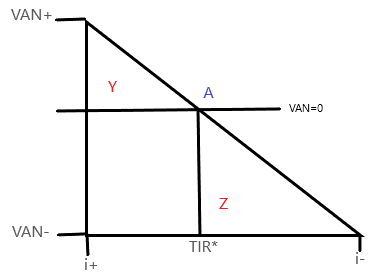
Mirando el triángulo con lupa, la ley de semjanza indica que todos los triángulos son proporcionales, entonces tanto el triángulo principal como el Y y el Z son proporcionales.
Esto indica que la relación de base y altura es la misma, tal que la división de la base entre la altura o viceversa entre los tres triángulos es igual, tal que, por ejemplo:
\frac{VAN_+\,+\, |VAN_-|}{i_-- \, i_+}=\frac{VAN_+}{TIR^*-\,i_+}=\frac{|VAN_-|}{i_--TIR^*}El primer término se refiere al triángulo grande, el de en medio al Y, y el final al Z. Lo único que hay que hacer en este caso es una vez conocidos todos los datos despejar el TIR*.
Un truquillo para ajustar más y facilitar el cálculo es hacer la diferencia de las tasa i- e i+ de tan solo un 1%, por tanto, el primer denominador desaparece.
Para hacer esto hay que hacerlo por tanteo, por prueba y error hasta encontrar estas dos cifras, de tal modo que en nuestro ejemplo VAN+=7,67 con i+=22%, mientras que VAN-=-8,09 al 23% de interés.
Por tanto, siguiendo como ejemplo el triángulo A, tenemos que:
\frac{7,67+8,09}{23\%-22\%}=\frac{7,67}{TIR^*-22\%}Al despejar TIR* tenemos que:
TIR^*=\frac{7,67 \, \cdot\,1\%}{7,67+8,09}+22\%=22,48\%Esta es una aproximación, pero aun podemos ir más allá si ajustamos un poquito más y tomamos este valor, el TIR*, como el límite superior, y calculamos un nuevo triángulo.
Cuantas más veces se haga este ajuste, menor error habrá, aunque el ajuste, como veremos a continuación, es bastante bueno.
Calcular la TIR en hoja de cálculo
Sin duda, los ejemplos anteriores son muy sencillos, y un ejemplo real de un proyecto es mucho más completo y difícil hacer el cálculo sin apoyo externo.
Este apoyo externo lo dan las hojas de cálculo y voy a mostrarte cómo calcular el ejemplo anterior con Excel y Google Sheets.
En realidad voy a mostrarte una alternativa a la función que te permiten las hojas de cálculo, donde tan solo debes anotar todos los flujos, seleccionarlos y usar la función «TIR».
A veces necesitas más información, o no puedes hacerlo de esa manera, y por eso te muestro a continuación cómo hacerlo de otra manera.
Tasa interna de retorno en Excel
Para encontrar el TIR en Excel primero se ha de calcular el VAN y usar la función de «Buscar objetivo» que se encuentra en la pestaña «Datos».
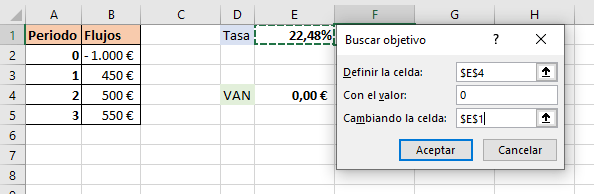
Hay que decir a Excel que busque la tasa, en este caso el TIR, que hace que el VAN sea 0, y te arroja el resultado.
Como se puede observar, esto lo hace muy rápido, y el resultado es igual a cuando calculamos en el apartado anterior la aproximación lineal y el TIR*.
En realidad no es igual, porque el resto de decimales que sigue cambia, pero la aproximación es muy ajustada, de tan solo un 0,003370928%.
En concepto de VAN, es un ajuste de 5 céntimos.
TIR en Google Sheets
El procedimiento es el mismo que en Excel con la salvedad de que la función no viene integrada y hay que descargar un complemento que permita hacerlo.
El complemento a descargar se llama «Goal Seek», que luego tendrás que abrir desde la pestaña complementos.
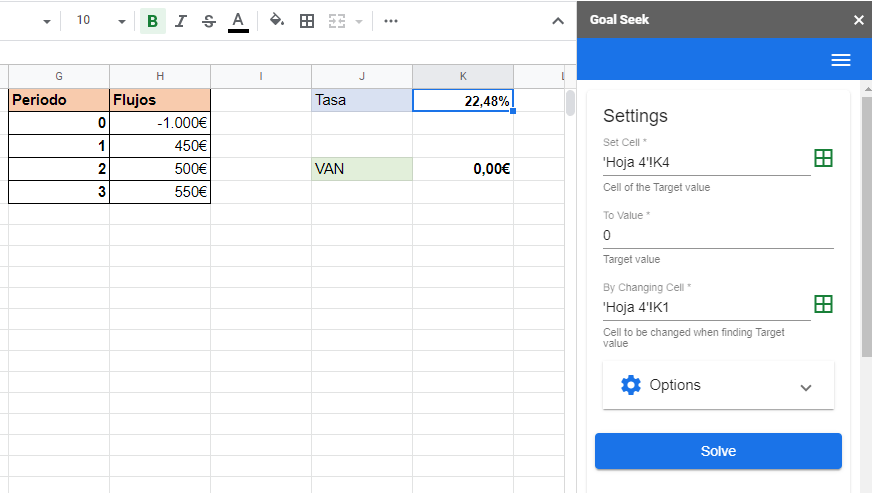
Con esta función es mucho más visible cómo lo que hace la herramienta es hacer búsqueda y error, es decir, hacer aproximaciones lineales hasta encontrar el punto óptimo.
¿Cómo vas a calcular la Tasa Interna de Retorno?
Ya tienes la TIR calculada, pero, ¿cómo la interprestas?
Como ves, hay diversidad de formas de calcular el TIR, aunque la hoja de cálculo te permite calcular cualquiera, pero quería mostrarte cómo puedes calcularlo a mano.
No sé si habrá un momento en el cual no dispongas de un dispositivo para hacer un cálculo rápido, pero sabiendo las diferentes técnicas nunca tendrás excusa.



Buenos días .
Muy clara la información excelente.
buena