Cuando realizamos una inversión, lo que más nos interesa saber es cuál va a ser nuestro beneficio en términos absolutos, pero más importante, en porcentaje, para poder comparar inversiones.
Para calcular el interés compuesto de una inversión se deben sumar todos los flujos actualizados y luego buscar la tasa de interés. El cálculo exacto se realiza con herramientas como una hoja de cálculo o calculadoras expresas para ello, aunque se puede hacer una aproximación a mano.
A continuación, te voy a comentar cómo calcular el interés compuesto de diferentes tipos de inversiones, así como contarte dónde se aplica o puedes usar el interés compuesto.
Calcular interés compuesto de una inversión
Aquí hablar de despejar la i y que es una inversión simple
Vamos a empezar el cálculo del interés compuesto de una inversión simple, la más simple posible, y vamos a comenzar analizando la capitalización compuesta con su fórmula.
C_n=C_0*(1+i)^n
La fórmula anterior nos dice que el capital en un momento, C_n, del tiempo, es igual al capital que se invierte hoy, C_0, multiplicado por el multiplicador del interés compuesto, (1+i)^n.
Por ejemplo, imagina que inviertes hoy 10.000€ al 10% de interés compuesto y quieres saber cuánto dinero tendrás en 5 años, entonces,
C_n=10.000*(1+10\%)^5=16.105,10€
Pero lo que nos interesa a nosotros es calcular la tasa de interés compuesto en una inversión, por ejemplo, imagina que ahora tienes 10.000€ para invertir y que dentro de 25 años quieres que ese capital sea de 45.000€, entonces, ¿a qué tasa debes invertir?
Para ello, de la fórmula anterior hay que despejar la i, de tal forma que,
i=\sqrt[n]{\frac{C_n}{C_0}}-1Si lo aplicamos al ejemplo anterior,
i=\sqrt[25]{\frac{45.000}{10.000}}-1=6,20\%Para lograr el objetivo, se necesita un interés compuesto anual del 6,20%.
Y esa es la forma de calcular en una inversión simple el interés compuesto, pero claro, la cosa se complica si analizamos otro tipo de inversiones, bien sean financieras o empresariales.
¿Qué es un interés compuesto sobre una inversión?
Es muy raro que en cualquier inversión el interés que se obtenga sea el mismo año tras año, o mes tras mes, sino que es variable (en muchos casos).
Al calcular el interés compuesto de una inversión, se consiguen dos cosas:
- Obtener el tipo de interés medio anual de esa inversión.
- Ese tipo de interés compuesto se calcula teniendo en cuenta la reinversión de los intereses.
Te pongo un ejemplo gráfico,

Si te interesa, consiste en mi inversión en Indexa Capital, donde invierto en carteras de fondos de inversión.
Como ves, cada mes la rentabilidad es variable, incluso en septiembre fue negativa, pero si lo analizamos en su conjunto, ¿cuál ha sido la rentabilidad compuesta media?
Eso es lo que se calcula cuando buscamos el interés compuesto sobre una inversión, que es lo que te he contado en el apartado anterior.
Inversión financiera con aportaciones
Ahora, vamos a calcular el tipo de interés compuesto de un producto de ahorro e inversión básico y muy común, como puede ser la inversión en fondos o planes de inversiones.
Si quieres
En este tipo de inversiones, se mete un capital inicial y luego se realizan aportaciones mensuales.
Por ejemplo, inviertes 10.000€ que tienes ahorrados y cada mes destinas 250€ extra que se van acumulando.
A su vez, como dije al principio, todos los intereses generados se van reinvirtiendo, lo cual es característico del interés compuesto.
Para evaluar este tipo de inversiones (o casi cualquiera) se deben calcular todos los flujos al valor actual, es decir, el valor actual neto de la inversión o VAN.
V_0=-C_0-F*\frac{1-(1+i)^{-n}}{i}+C_f*(1+i)^{-n}=0Para obtener la i, el valor actual debe igualarse a cero, esto también se conoce como calcular la tasa interna de retorno de una inversión.
Lo que tenemos en la fórmula anterior es el capital inicial, lo que se invierte hoy, que ya está actualizado, y luego una fórmula de actualización, que no es menester que te la explique aquí, pero lo que hace es actualizar una renta donde todos los flujos son iguales, en nuestro caso, las aportaciones mensuales. Y el Capital final objetivo que queremos lograr.
Si en tu cálculo cambiases esas aportaciones, deberías reajustar la fórmula, así que la anterior solo sirve si se mantienen los mismos flujos en todo el periodo.
Ahora, vamos a seguir con el ejemplo anterior si la inversión dura 10 años, y tu objetivo es lograr 50.000€,
V_0=-10.000-250*\frac{1-(1+i_{12})^{-120}}{i_{12}}+50.000*(1+i_{12})^{-120}=0Los desembolsos que hacemos están en negativo porque salen de nuestro bolsillo, es lo que pagamos, mientras el capital final que esperamos lograr está en positivo, porque es lo que ganamos, lo que nos entra, futuros ingresos.
La particularidad en este caso, es que la tasa que se calcula es la mensual, puesto que los flujos son mensuales, y una vez la obtengamos debemos calcular el interés anual.
Ahora, vamos a ver cómo se calcula en Excel, porque también se puede hacer a mano, pero lo dejo para los más atrevidos.
Calcular en Excel la tasa de interés compuesto de una inversión con aportaciones mensuales
Lo primero de todo es poner los datos en la hoja de cálculo como se muestra en la imagen siguiente:
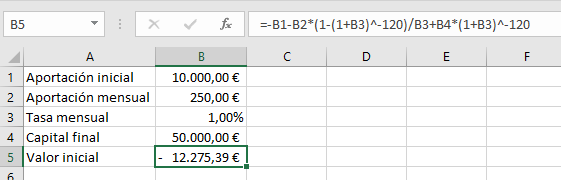
La fórmula que aparece es la que está fijada en la celda B5, que es el valor actual con un 1% mensual, que es una cifra que he puesto de ejemplo, y que ahora calcularemos una vez están todos los datos en Excel.
El siguiente paso es ir a la función de buscar objetivo, para ello debemos ir a Datos > Análisis de hipótesis > Buscar objetivo.
Aparece una nueva ventana que nos va a servir para hacer el cálculo de la tasa de interés.
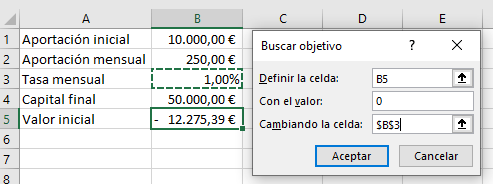
Lo que decimos, es que nos busque aquella tasa de interés mensual, que haga que el valor actual sea cero, y eso es lo que está dispuesto en la ventana emergente.
Entiende que el interés que se calcula es el mensual porque las aportaciones son mensuales, si fuesen aportaciones anuales, el interés sería anual.
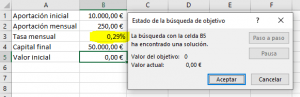
Una vez clicamos Aceptar, ya realiza el cálculo con aproximación lineal, vamos que hace prueba y error hasta acercarse al objetivo.
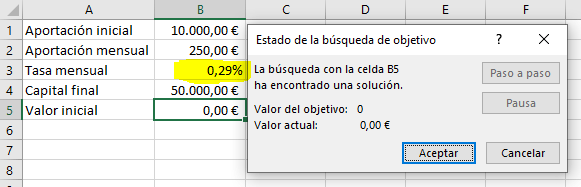
En este caso obtenemos que, con el ejercicio planteado, se consigue un 0,29% de tipo de interés compuesto mensual, aunque siempre conviene obtener la tasa anual, que nos permite mejor comprar entre inversiones.
Para ello se aplica la fórmula de equivalencia de tantos en interés compuesto, que es la siguiente,
i=(1+i_{12})^{12}-1En nuestro caso, aplicamos esta fórmula en Excel para obtenerlo de manera inmediata por si hacemos cualquier cambio.
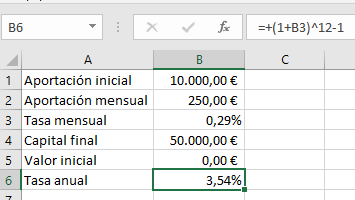
En este caso, obtenemos que el tipo de interés compuesto anual de una inversión con aportaciones mensuales y un objetivo de capital futuro es del 3,54% anual.
Inversión empresarial
En realidad, calcular el tipo de interés de una inversión empresarial tiene la misma alma mater que el caso anterior, solo que, con mayor complejidad, puesto que hay muchos flujos de diferente periodicidad.
Es decir, un proyecto empresarial tiene ingresos en diferentes periodos, mensuales, a 90 días, semestrales, así como gastos e inversiones a lo largo de todo el proyecto.
Así que lo que se debe hacer es lo mismo que antes, solo que en cada caso la fórmula a calcular es diferente puesto que los flujos serán también distintos.
En definitiva, se deben llevar todos los flujos al periodo actual, y desde ahí buscar la tasa de interés compuesto anual como hemos hecho buscando objetivo en Excel.
Vamos a verlo con un ejemplo sencillo, muy típico en España, que es montar un bar.
Primero se tiene un desembolso inicial para rehabilitar el local de 75.000€, más unos gastos de alquiler mensuales de 1.000€ y de personal de 4.500€. Hay gastos anuales de seguros y demás de unos 9.000€.
En cuanto a los ingresos, se prevé una facturación mensual neta de 8.000€, aquí lo vamos a hacer con unos ingresos constantes para que el cálculo sea más sencillo, aunque sabemos que no es así.
Si consideramos que la inversión es de 10 años y no tiene valor residual,
V_0=-75.000+(8.000-1.000-4.500)*\frac{1-(1+i_{12})^{-120}}{i_{12}}-9.000*(1+i)^{-10}No voy a hacer este cálculo en Excel, pero puedes llevar los mismos pasos que antes, aunque ahora debes ajustar el último flujo a mensual, o puedes usar una tasa diferente en cada caso.
El resultado, por si lo quieres comprobar es i=31,24\%, y i_{12}=2,29\%.
Una rentabilidad jugosa, pero es solo un ejemplo.
Hay que entender que cualquier inversión empresarial va a tener muchísimos más componentes con diversa periodicidad que lo hace más complejo, aunque igual de sencillo.
Riesgos del interés compuesto
El principal riesgo que asumimos cuando calculamos la tasa de interés compuesto es que asumimos que todos los flujos se reinvierten a la misma tasa, lo cual no es cierto.
En muchos casos, los flujos no se reinvierten, como en la mayoría de inversiones empresariales, donde todas las ganancias no se reinvierten para obtener una rentabilidad.
Además, como hemos visto en mi ejemplo, las tasas no se mantienen constantes a lo largo del tiempo, sino que fluctúan.
Estos elementos se han de tener en cuenta para entender qué estamos calculando y para qué nos sirve.
Sin duda, hacer estos cálculos nos va a permitir tomar mejores decisiones de inversión, pero nada mejor que entender qué se está haciendo para no caer en errores que nos lleven a obtener resultados no esperados.
¿Dónde puedes aplicar el interés compuesto?
Creo que ya te podrás hacer una idea de dónde se aplica el interés compuesto, y cómo calcularlo en varios casos.
Más bien, podemos decir que no se aplica en aquellos casos donde los intereses no se reinvierten, que hoy en día son cada vez menos comunes.
Así, en líneas generales, decimos que el interés compuesto se puede aplicar en:
- Cuentas bancarias de ahorro que arrojen una rentabilidad
- Inversiones en fondos de inversiones o carteras de fondos
- Ahorro en planes de pensiones
- Inversión en value investing en acciones de empresas
- Inversión en bonos corporativos y públicos
- Cálculo de inversiones empresariales
- La hipoteca de la casa
- Los intereses de la tarjeta de crédito
- …
Seguramente haya muchos más usos para aplicar el interés compuesto, sin duda, los usos principales son el de valorar inversiones y tomar decisiones de inversión.
El cálculo del tipo de interés no dice nada a menos que apliquemos inteligencia financiera que nos lleve a obtener rendimientos positivos y con reducido riesgo.
Puntos clave
A menudo necesitamos calcular el interés compuesto de una inversión para poder decidir si la llevamos a cabo, si necesitamos buscar otras inversiones alternativas, o bien nos retiramos.
Estos son los principales puntos clave del artículo:
- El cálculo del interés compuesto nos permite conocer cuál es el tipo de interés medio anual de una inversión, y así poder comparar entre inversiones.
- El interés compuesto tiene en cuenta que los intereses generados se reinvierten todos a una misma tasa.
- Además, la tasa es invariable a lo largo del tiempo, aunque esto solo sea en el cálculo, no en la práctica.
- Calcular la tasa de interés compuesto se asemeja al cálculo de la tasa interna de rentabilidad de una inversión.
- El interés compuesto se aplica a numerosos productos financieros que forman parte de nuestro día a día.
Espero que con toda esta información tengas más claro cómo calcular el interés compuesto ante cualquier inversión que se te plantee, y también te sirve para hacer simulaciones y búsqueda de objetivos financieros.
Si tienes cualquier duda o necesitas aclaración, agrégalo a los comentarios.