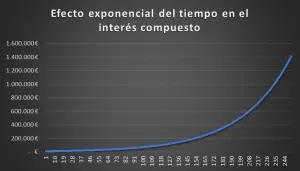
Al planificar las finanzas personales a largo plazo, uno de los componentes que necesitamos conocer es el tiempo que nos llevará conseguir nuestros objetivos.
Imagina que tienes el objetivo de conseguir 100.000€ con una inversión de 25.000€ a un 5% de rendimiento anual, entonces, ¿cuánto tiempo te llevará conseguirlo?
Para calcular el tiempo en interés compuesto debemos despejar la variable tiempo de la fórmula de capitalización con interés compuesto, tal que, n=\frac{log C_n - log C_0}{log (1+i)}.
Sigue leyendo porque te voy a mostrar en detalle a cómo calcular el tiempo a mano y a ordenador por si te eres más tecnológico, además de mostrarte ejemplos para que lo entiendas y lo apliques.
Calcular el tiempo en interés compuesto
Calcular el tiempo en interés compuesto es un elemento esencial para planificar inversiones, tanto si son empresariales como personales. Es un elemento clave, por ejemplo, para calcular la jubilación.
¿Cuál es la fórmula para calcular el tiempo en interés compuesto?
Como comentaba al principio, se ha de partir de la fórmula de capitalización compuesta para poder despejar el factor tiempo y así calcularlo.
La fórmula de capitalización con interés compuesto es la siguiente:
C_n=C_0*(1+i)^n
Puesto que el tiempo, n, está en el exponente, hay que hacer una serie de ajustes con logaritmos para poder bajar el exponente y despejarlo. Lo vemos en la siguiente secuencia:
C_n=C_0*(1+i)^n\\ log\,C_n=log\,C_0*(1+i)^n\\ log \,C_n=log\,C_0+log\,(1+i)^n\\ log\,C_n-log\,C_0=n*log\,(1+i)
Una vez llegados a este punto, el último paso es despejar n para tener la fórmula necesaria para calcular el tiempo con interés compuesto:
n=\frac{log C_n - log C_0}{log (1+i)}Ya tenemos la fórmula para calcular el tiempo con interés compuesto a mano, bueno, más bien se puede calcular con cualquier calculadora de forma muy sencilla, hasta incluso con tu teléfono móvil puedes hacerlo.
Aunque quizás te interese también saber cómo calcularlo con Excel, puesto que te va a ahorrar tiempo si decides hacer muchos cálculos en menos tiempo.
Cálculo en Excel
Lo principal es escribir en el Excel todos los parámetros necesarios que están en la fórmula. Siguiendo el ejemplo anterior:
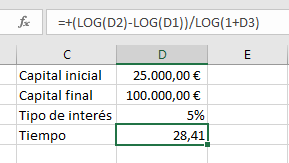
Como puedes observar, en la celda Tiempo está escrita la fórmula anterior.
El ejemplo nos dice que se necesitarían casi 28 años y medio para alcanzar el objetivo.
Lo bueno que nos permite Excel, es que podemos cambiar cualquier parámetro, por ejemplo, el tipo de interés, y el cálculo es automático, lo que te va a permitir tomar mejores decisiones financieras.
Más adelante veremos ejemplos para analizar cómo afecta cada parámetro.
¿Qué es el tiempo en el interés compuesto?
Comentar el efecto del tiempo y la curva exponencial.
El tiempo no es más que los periodos que se necesitan para alcanzar un capital objetivo partiendo de un capital invertido.
Es importante diferenciar entre tiempo o periodos, porque realmente lo que se calcula con la fórmula son los periodos, n, el tiempo en realidad dependerá de cómo sea el tipo de interés.
En el ejemplo anterior hemos usado un interés anual, por lo que el tiempo es en años, pero si usáramos un interés mensual, el resultado serían meses.
Por ejemplo, la cartera de fondos de inversión donde yo invierto me proporciona las rentabilidades mensuales.
Imagina que invierto 10.000€ y quiero ver cuánto tiempo tarda en duplicarse mi capital si el tipo de interés es del 2% mensual. Veamos el tiempo:

El tiempo en duplicarse sería de 35 meses, es decir, 3 años menos un mes. Como ves, la fórmula funciona igual, tan solo debes ser consciente de qué datos estás introduciendo.
Por cierto, si quieres invertir en carteras de fondos de inversión como yo, y lo haces a través de Indexa clicando en este enlace, te bonifican sin costes de gestión durante un año en los primeros 10.000€ de inversión.
Y es que el tiempo en interés compuesto es clave, puesto que el interés compuesto crece de manera exponencial, así que cuanto más pase el tiempo, el crecimiento del capital se dispara.
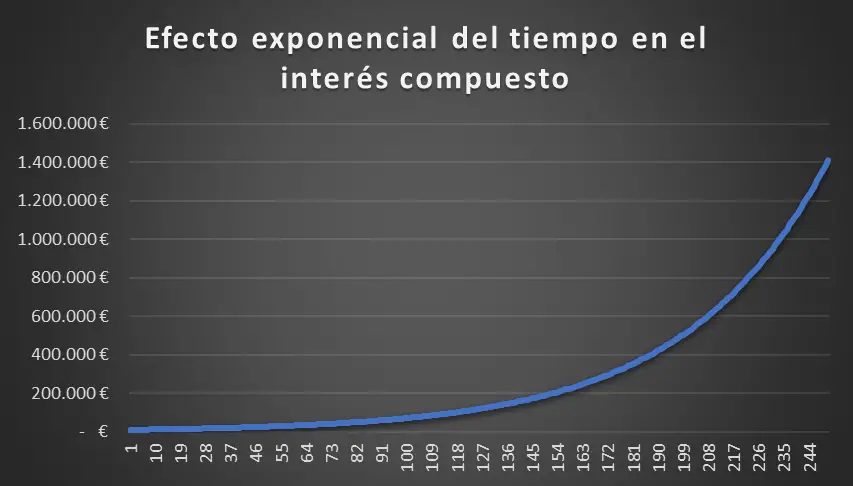
Al principio el crecimiento es lento, pero la particularidad del interés compuesto es que los intereses generan a su vez más intereses, por tanto, conforme los intereses crecen, el crecimiento se vuelve exponencial.
Por ello es importante comenzar a ahorrar o invertir cuanto antes para aprovechar este efecto del tiempo en la capitalización compuesta.
Ejemplos de cálculo del tiempo en interés compuesto
Cualquier ejemplo te va a servir para practicar como ejercicios. Aunque ya has visto un par de ejemplos útiles y cómo cambiar los parámetros en Excel para que el cálculo sea inmediato.
En realidad, para calcular el tiempo hay tres parámetros: el capital objetivo o final, la inversión inicial, y el tipo de interés.
La fórmula, n=\frac{log C_n - log C_0}{log (1+i)}, nos indica cómo afectan los movimientos de cada elemento.
Por ejemplo, si aumentamos el capital objetivo, el tiempo para lograr el objetivo aumenta:
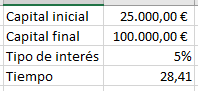
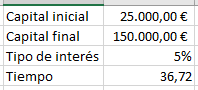
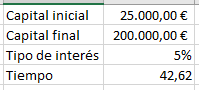
Se observa como el tiempo aumenta, aunque debido al efecto del interés compuesto, el aumento es cada vez menor, ante una misma subida de capital.
Ahora, si aumentamos el capital inicial, obviamente el esfuerzo para alcanzar el objetivo es menor:

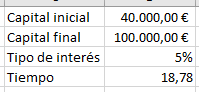
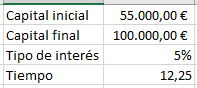
Se puede comprobar cómo el tiempo se reduce.
Por último, queda comprobar cómo afecta el tipo de interés, aunque se puede ver que, al estar en el denominador, si aumenta el tipo de interés, disminuye el tiempo:

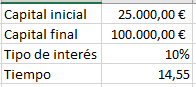
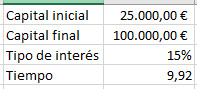
Como se aprecia en los ejemplos, se cumple lo esperado.
Tienes ejemplos que te pueden servir para practicar como ejercicios, que los puedes calcular con tu calculadora o tu móvil.
Cómo se calcula el tiempo en el interés simple
Es común comparar el interés compuesto con el interés simple, ya que son las dos capitalizaciones más usadas en finanzas, aunque la compuesta gane por goleada.
Como anteriormente, de la fórmula de la capitalización simple hay que despejar el tiempo, que en este caso es mucho más sencillo. Veamos,
C_n=C_0*(1+i*n)\\
\frac{C_n}{C_0}=1+i*n\\
n=\frac{\frac{C_n}{C_0}-1}{i}Como se puede observar, no hace falta usar logaritmos ni nada raro para lograr la fórmula para calcular el tiempo con interés simple.
Si en el Excel anterior introducimos esta nueva fórmula, podemos ver la diferencia entre las diferentes capitalizaciones, o calcularla en el caso de que quieras invertir en productos que te ofrezcan este tipo de intereses.
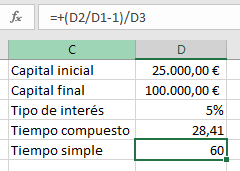
Se tarda más del doble de años en lograr el objetivo con capitalización simple que con compuesta.
Puedes ver en estos cálculos el poder del interés compuesto y también calcular las diferencias en los ejemplos anteriores.
Es tu interés
Conocer, entender y saber calcular cualquier elemento del interés compuesto está en tu interés, presente y futuro.
Ante situaciones cada vez más cambiantes y con mayores incógnitas, es esencial hacer una buena planificación para cumplir con los objetivos financieros a largo plazo.
Estos son los puntos clave de este artículo:
- El tiempo para alcanzar tus objetivos financieros depende de cuál sea el objetivo, el capital inicial que puedas invertir, y el tipo de interés o rendimiento que consigas.
- Hacer diferentes pruebas y test te va a permitir tomar mejores decisiones de inversión.
- El efecto del interés compuesto se aprecia mejor en el largo plazo, así que ahora es el momento de empezar a invertir.
Si tienes cualquier duda o necesitas alguna aclaración no dudes de comentarlo en los comentarios.