Te han dado el interés que debes pagar o que vas a cobrar por esa nueva inversión que acabas de hacer, pero te han dado el interés anual, cuando los flujos son mensuales.
A veces es tan sencillo como hacer una simple decisión, pero no suele ser tan sencillo.
Suscríbete: Ivoox | Itunes | Spotify | | Podimo
Los tantos equivalentes te permiten calcular los tipos de interés para diferentes periodos de tiempo como mensual, trimestral, bimensual, semestral, etc.
Por eso te voy a contar cómo calcular estos tantos si tu interés es simple o compuesto.
Tantos equivalentes para interés simple
Como el nombre indica, es muy simple, para obtener el tipo de interés expresado en otro periodo de tiempo, tan solo hay que hacer una división del tipo de interés anual.
Por ejemplo, y para hacerlo sencillo, si el tipo de interés anual es del 12%, el tipo de interés mensual es del 1%, porque un año tiene 12 meses.
Si es trimestral, habrá que dividir entre 4 porque un año tiene 4 trimestres, por lo que el interés simple trimestral será del 3%, que a su vez es la multiplicación del interés simple mensual por 3.
En este caso la simplicidad es lo que rige el cálculo.
Tantos equivalentes para el interés compuesto
En este caso el cálculo es más complicado, pero también es sencillo, aunque no tanto.
Cabe recordar que el interés compuesto vuelve a reinvertir los intereses cobrados, y de ahí radica la principal diferencia.
Lo que se hace es que se ha de buscar el tipo de interés que es equivalente con el anual y con el que se obtenga el mismo resultado.
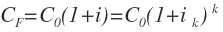
Esta fórmula nos indica que el capital final debe ser el mismo tanto si el tipo de interés es anual, como si está expresado en otro momento del tiempo.
En este caso, «k» expresa el periodo de tiempo, por lo tanto debemos encontrar ese tipo de interés porque el anual es el conocido, así que solo hay que despejar el interés en tiempo k de esta igualdad:
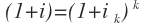
Una vez despejamos ya se pueden calcular los tantos equivalentes para el interés compuesto, tal que:
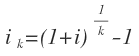
Siguiendo el ejemplo anterior de un 12% anual, el tanto mensual en este caso es del 0,95%, menos que en el interés simple, pero porque hay reinversión de los intereses.
A su vez, el trimestral es del 2,87%, también inferior al 3% anterior.
Es una fórmula muy útil para saber la rentabilidad real que puedes conseguir al invertir en interés compuesto, debido a que la mayoría de inversiones se actualiza mensual o incluso de forma diaria.
En definitiva
Conocer la ley de los tantos equivalentes es esencial para conocer los tipos de interés en diferentes momentos del tiempo.
A su vez, dependiendo del proyecto de inversión que tengas entre manos te permite diferenciar entre tipos de interés simple y compuesto.
En definitiva, saber dirimir entre proyectos con tipos de interés de diferente duración te permite seleccionar aquella oportunidad que te aporte una mayor rentabilidad.


