Una situación que se nos presenta en nuestra vida es la de conocer cuánto dinero necesitamos para jubilarnos. Si estás pensando en comenzar a ahorrar, es interesante que conozcas cómo calcular el capital final si lo haces con interés compuesto.
A su vez, también te puede interesar conocerlo en el caso de que quieras ahorrar para comprar una casa, un coche, o darte un capricho en el corto o medio plazo.
Para calcular el capital final se multiplica el capital inicial a invertir por la capitalización de cada periodo. Por tanto, se necesita conocer la inversión inicial, el tipo de interés de cada periodo, y el número de periodos o duración de la inversión.
Quédate hasta el final porque te voy a contar con todo detalle cómo calcular el capital final con interés compuesto, además de mostrarte las diferencias si la capitalización es simple, y si ya sabes cuánto dinero quieres conseguir, te enseño a calcular el tipo de interés mínimo que necesitas para lograrlo.
Calcular el capital final con interés compuesto
Para calcular el capital final con interés compuesto normalmente se usa una fórmula estándar, pero solo funciona bajo el supuesto de que el tipo de interés es el mismo para toda la duración de la inversión.
Esta fórmula es la siguiente:
C_f=C_0*(1+i)^n
Donde C_f es el capital final, es decir, el dinero que pretendemos conseguir cuando se acabe la inversión. C_0 es el dinero que se quiere invertir, o el capital inicial en el momento 0. La letra i es el tipo de interés que se obtiene como beneficio. Y la n es el número de periodos que dura la inversión.
Pero como decía, esta fórmula solo es viable siempre y cuando el tipo de interés, i , sea el mismo en todos los periodos. ¿Qué pasa cuando no lo es? Veamos de dónde nace esta fórmula.
La base del interés compuesto es que los intereses también se capitalizan, es decir, que se reinvierten y se consiguen a su vez intereses de los intereses.
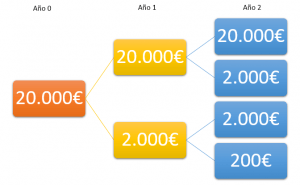
Como ejemplo, imagina que inviertes 20.000€ al 10% anual, por tanto, al año siguiente el capital del que dispones es de los 20.000€ más 2.000€ de intereses. Al siguiente año, tanto el capital inicial como los intereses del primer año generan de nuevo intereses. Y así durante todo el periodo de inversión.
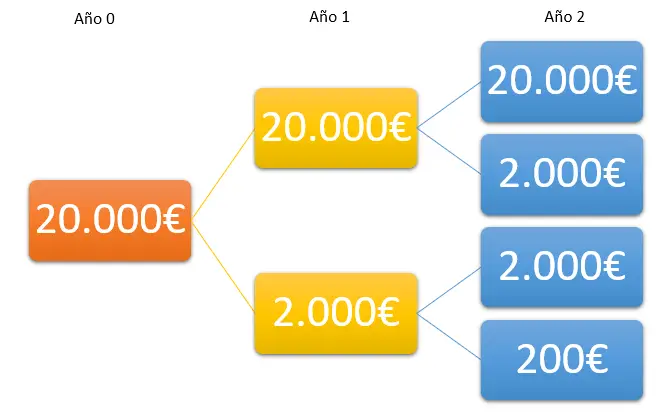
La imagen anterior muestra cómo evoluciona el capital con el paso de los periodos. Veamos la evolución de forma analítica periodo a periodo.
C_1=C_0+C_0*i_1=C_0(1+i_1)\\ C_2=C_1(1+i_2)=C_0(1+i_1)(1+i_2)\\ C_3=C_2(1+i_3)=C_0(1+i_1)(1+i_2)(1+i_3)\\ ...\\ C_n=C_0(1+i_1)(1+i_2)...(1+i_n)
Como se observa en la ecuación anterior, para calcular el capital en cualquier periodo, incluso el final, se multiplica el capital invertido por la capitalización de cada periodo. Pongamos un ejemplo al invertir un capital de 20.000€ durante tres años y el siguiente esquema de tipos de interés.
| Periodo | Tipo de interés |
| 1 | 5% |
| 2 | 7% |
| 3 | 10% |
Si introducimos los datos en la fórmula anterior:
C_f=C_3=20.000*1,05*1,07*1,1=24.717
De esta forma se calcula el capital final con interés compuesto, aunque hay un atajo en el caso que el tipo de interés sea el mismo en cada periodo, logrando como resultado la primera fórmula.
Se llega de la siguiente manera:
C_1=C_0+C_0*i=C_0(1+i)\\ C_2=C_1(1+i)=C_0(1+i)(1+i)=C_0(1+i)^2\\ C_3=C_2(1+i)=C_0(1+i)^2(1+i)=C_0(1+i)^3\\ ...\\ C_n=C_0(1+i)^n
Si calculamos el ejemplo de una inversión de 20.000€ al 10% anual durante 3 años:
C_f=20.000*1,1^3=26.620
Espero que ya tengas un mejor conocimiento de cómo calcular el capital final con interés compuesto en todas las situaciones posibles. No obstante, te voy a dejar con ejemplos para que te familiarices con la metodología.
2 ejemplos de aplicación del interés compuesto
A continuación, te voy a mostrar dos ejemplos reales de aplicación del interés compuesto que se han dado en mi caso. El primero es un caso donde el interés no varía a lo largo de un año, mientras que en el segundo caso sí lo hace.
Cuenta corriente remunerada
El primer ejemplo es el de una cuenta corriente remunerada o cuenta de ahorros.
Vamos, una cuenta en un banco que te da un interés por el dinero que tienes depositado, algo con lo que siempre hemos vivido.
En este caso es la cuenta de Myinvestor que remunera al 1% anual una cantidad de hasta 15.000€, es decir, que si tienes 25.000€ solo te paga intereses por los primeros 15.000€.
Aunque el interés que siempre están obligados de mostrar bancos y otras entidades financieras sea anual, eso no significa necesariamente que lo paguen en ese periodo.
Normalmente, las cuentas pagan los intereses mes a mes, por tanto, en un año hay 12 periodos, lo que nos sirve para calcular este ejercicio.
Para este ejemplo, tampoco nos sirve usar un capital superior a 15.000€, porque si no los intereses no se reinvertirían, y estaríamos ante una situación similar a la capitalización simple.
Imagina que con las condiciones mostradas (1% anual con devengo mensual) decides ahorrar 10.000€ en esta cuenta, ¿cúanto capital tendrías al año que viene cuando acaba la oferta?
En realidad, es muy sencillo el cálculo:
C_f=C_0*(1+i)=10.000*1,01=10.100€
Pero como he indicado anteriormente, el devengo es mensual, por lo que en tu cuenta corriente habrán reflejados 12 pagos que entre todos sumen 100€ de interés que ganarías. Así quedaría la tabla de pagos:
| Mes | Capital | Intereses |
| 0 | 10.000,00 € | |
| 1 | 10.008,30 € | 8,30 € |
| 2 | 10.016,60 € | 8,30 € |
| 3 | 10.024,91 € | 8,31 € |
| 4 | 10.033,22 € | 8,32 € |
| 5 | 10.041,55 € | 8,32 € |
| 6 | 10.049,88 € | 8,33 € |
| 7 | 10.058,21 € | 8,34 € |
| 8 | 10.066,56 € | 8,34 € |
| 9 | 10.074,91 € | 8,35 € |
| 10 | 10.083,26 € | 8,36 € |
| 11 | 10.091,63 € | 8,36 € |
| 12 | 10.100,00 € | 8,37 € |
| 100,00 € |
Se observa cómo al ser interés compuesto, conforme va pasando el tiempo los intereses generados crecen. Como es un periodo corto y el interés es bajito no se aprecia un gran crecimiento, pero este es exponencial.
Al final del año se han generado 100€ de beneficio que se han pagado mes a mes, pero el importe de cada mes varía.
Además, como el tipo de interés es el mismo durante todo el periodo, se podría usar la fórmula de cálculo del capital final que hemos visto al principio, con la consideración de que el tipo de interés es mensual:
C_f=C_0*(1+i_{12})^{12}=10.000*1,008^{12}=10.100€Hay diferentes caminos para llegar al mismo lugar si se saben usar las matemáticas apropiadamente.
Carteras de fondos de inversión
Otra manera con la que ahorro de forma pasiva es a través de las carteras de fondos de inversión.
Lo hago a través de Indexa Capital y te voy a mostrar el cuadro de rendimientos real de mi cuenta durante el año pasado.

Como se puede observar, las rentabilidades son diferentes mes a mes, e incluso hay rentabilidades positivas y negativas. El año 2020 fue un poco loco, diferente, y de ahí la variabilidad de la rentabilidad.
Si aplicamos esta rentabilidad a un capital de 10.000€ como antes tendríamos lo siguiente:
| Mes | Capital | Intereses |
| 0 | 10.000,00 € | |
| 1 | 10.210,00 € | 210,00 € |
| 2 | 9.648,45 € | -561,55 € |
| 3 | 8.616,07 € | -1.032,38 € |
| 4 | 9.391,51 € | 775,45 € |
| 5 | 9.541,78 € | 150,26 € |
| 6 | 9.522,69 € | -19,08 € |
| 7 | 9.627,44 € | 104,75 € |
| 8 | 10.002,91 € | 375,47 € |
| 9 | 9.842,87 € | -160,05 € |
| 10 | 9.754,28 € | -88,59 € |
| 11 | 10.446,83 € | 692,55 € |
| 12 | 10.478,17 € | 31,34 € |
| 478,17 € |
A pesar de los altibajos, la rentabilidad final fue positiva, ya que se puede observar que hay un beneficio.
Este ejemplo muestra que el beneficio de la capitalización compuesta también se puede volver en tu contra si las rentabilidades son negativas y se acumulan periodo a periodo.
Para el cálculo de esta operación deberíamos usar la segunda ecuación del texto tal que,
C_f=C_0(1+i_1)(1+i_2)...(1+i_{12})=\\
=10.000*1,021*0,945*...*1,003=10.478,17€Ya te he mostrado dos ejemplos sobre cómo calcular el capital final con interés compuesto tanto si el tipo de interés es fijo, como variable.
Por otro lado, si quieres ir a la parte práctica y saber cómo invertir en interés compuesto, aquí te dejo otro artículo mío.
Diferencias con el cálculo del capital final en interés simple
Cuando hablamos de capitalización simple, los intereses no se reinvierten, sino que se extraen.
Siguiendo el ejemplo inicial de invertir 20.000€ durante 3 años al 10% anual, cada año se obtendrían los intereses de 2.000€ que no se reinvierten, con un beneficio total de 6.000€.
Si lo vemos de forma analítica nos va a permitir comparar mejor con la capitalización compuesta:
C_1=C_0+C_0*i=C_0(1+i)\\ C_2=C_1+C_0*i=C_0(1+i)+C_0*i=C_0(1+2*i)\\ ...\\ C_n=C_0(1+n*i)
En la capitalización simple cada periodo se suma la tasa de interés a través de una progresión aritmética.
Al plasmar el ejemplo en la fórmula:
C_f=20.000*(1+3*10\%)=26.000€
En tan solo 3 periodos se puede observar que ya hay diferencias, puesto que la misma operación con capitalización compuesta daba un total de 26.620€.
El único periodo donde la capitalización simple y la compuesta son iguales es en el primero, donde todavía no se ha activado
Cómo calcular la tasa de interés compuesto
Hasta ahora hemos visto cómo calcular el capital final de una inversión, pero, ¿qué pasa si quieres conocer qué tipo de interés necesitas para alcanzar un capital deseado?
Imagina que tienes unos ahorros de 15.000€ y quieres invertirlos para tener 50.000€ dentro de 15 años. ¿Qué tipo de interés mínimo tienes que lograr para alcanzarlo?
Si atendemos a la fórmula de capitalización compuesta, C_f=C_0(1+i)^n , debemos despejar el tipo de interés para conocerlo. Haciendo un poco de magia potagia con las matemáticas tenemos que:
i=\sqrt[n]{\frac{C_f}{C_0}}-1Que aplicando el ejemplo tenemos que:
i=\sqrt[15]{\frac{50.000}{15.000}}-1=8,36%Si queremos alcanzar un capital de 50.000€ en 15 años invirtiendo 15.000€, debemos de buscar una rentabilidad anual mínima del 8,36%.
De este modo se cierra el círculo y se es capaz de calcular tanto el capital final, como el interés mínimo al que se debe invertir.
Reflexión final
El uso del interés compuesto forma parte de nuestras vidas, está en muchos elementos cotidianos como has podido observar.
Entender cómo funciona te va a servir para saber qué esperar o no de una inversión, además de cómo te afecta negativamente en el caso de que pidas dinero prestado.