Los servicios financieros ofrecen siempre el tipo de interés anual de todos los productos, porque es el tipo que nos permite compararlos a todos. Pero en muchas ocasiones el pago de intereses se hace de forma mensual y es por ello que queremos saber cuánto interés mensual nos van a liquidar, o tenemos nosotros que pagar.
Para calcular el tanto de interés compuesto en meses necesitas aplicar esta fórmula, i_{12}=(1+i)^{\frac{1}{12}}-1 . Donde i es el tipo de interés anual e i_{12} el mensual. Por ejemplo, si el tipo de interés anual es del 10%, i_{12}=(1+0,1)^{\frac{1}{12}}-1=0,7974 %.
A continuación, te voy a mostrar cómo puedes calcular el tipo de interés en cualquier periodo inferior a un año (meses, trimestres, semanas, días, …), así como enseñarte de dónde sale este concepto para que lo entiendas todo.
Cómo calcular el interés compuesto en meses
En definitiva, lo que buscamos es que tanto si el tipo de interés es anual como mensual, el resultado sea el mismo, es decir, que si tus ganancias han de ser de 1.000€, que consigas ese dinero da igual en qué periodos te paguen los intereses.
La fórmula de capitalización compuesta es la siguiente: C_f=C_0*(1+i)^n
En el caso de que apliquemos la fórmula de interés compuesto a un año, tendríamos lo siguiente, C_f=C_0*(1+i). (Lo único que cambia es que n=1).
Ahora, si aplicamos la fórmula para calcular el capital final con interés compuesto, tendríamos que C_f=C_0*(1+i_{12})^{12}. Donde i pasa a ser i_{12} porque hay 12 meses en un año, al igual que n=12 en este caso.
Por cierto, para entender definitivamente cómo calcular el capital final con interés compuesto pincha y lee este otro artículo.
Como decíamos al principio, el capital final que se obtenga en cada caso ha de ser igual, por tanto, si igualamos las fórmulas de cada capital final, anual y mensual, tenemos que:
C_0*(1+i)=C_0*(1+i_{12})^{12}Podemos simplificar la igualdad dividiendo ambos términos de la igualdad entre C_0 , obteniendo,
(1+i)=(1+i_{12})^{12}Para conseguir el interés compuesto mensual, tan solo queda despejar i_{12} , y para ello elevamos el término de la izquierda entre 1/12 y le restamos el 1 restante, tal que,
i_{12}=(1+i)^\frac{1}{12}-1Ahora sí, siempre que tengas el tipo de interés anual, lo puedes pasar fácilmente a tipo de interés compuesto mensual a través de esa fórmula, y viceversa, si lo que tienes es el tipo de interés mensual y quieres obtener el anual, debes despejar i, tal que,
i=(1+i_{12})^{12}-1Ejemplo de tipo de interés compuesto anual a mensual
Voy a poner un ejemplo, y luego te dejo con algunos datos para que puedas practicar.
Imagina que logras una rentabilidad anual en una cuenta de ahorros del 1% anual, ¿cuánto sería mensual?
i_{12}=(1+0,01)^\frac{1}{12}-1=0,08\%Ahora te dejo con una tabla para ver algunas características:
| i | i_{12} | i_{12}*12 |
| 1.00% | 0.08% | 0.9954% |
| 2.00% | 0.17% | 1.9819% |
| 3.00% | 0.25% | 2.9595% |
| 5.00% | 0.41% | 4.8889% |
| 10.00% | 0.80% | 9.5690% |
| 25.00% | 1.88% | 22.5231% |
| 50.00% | 3.44% | 41.2393% |
| 100.00% | 5.95% | 71.3557% |
Las dos primeras columnas te van a servir de datos para practicar la fórmula anterior, pero lo relevante es la tercera columna, que podemos decir que es el acumulado de los intereses durante todo el año.
Como se observa, el acumulado del interés compuesto es inferior al interés anual, es decir, si el anual es el 10% el acumulado del mensual es del 9,57%, diferencia cada vez mayor cuanto mayor sea el tipo de interés anual.
Esto es así, porque al hablar de interés compuesto, los intereses generados se reinvierten, por tanto, el capital va creciendo con cada pago y es por ello que se requiere un menor tipo de interés para alcanzar el mismo resultado.
Cómo calcular el interés compuesto en otros periodos
La fórmula para calcular el tipo de interés compuesto en periodos inferiores al año tiene su razón de ser.
En definitiva, sea cual sea el periodo del tipo de interés (anual, semestral, diario, …) lo que se busca es un mismo resultado, es decir, que dé igual aplicar uno u otro, que el resultado sea el mismo.
He comentado anteriormente, que la mayoría de productos financieros aplican el interés compuesto y, aunque para comparar se use el anual, su aplicación suele ser en periodos inferiores.
Por ejemplo, en el pago de una hipoteca que se hace mensual, al igual que si tienes una cuenta de ahorro en un banco que paga intereses mensuales.
Sea como sea, repito que lo que se busca es que el resultado sea el mismo, da igual cuál sea la periodicidad con la que se aplique el tipo de interés.
Es decir, imagina que inviertes (ahorras, pagas, …) 5.000€ con un tipo de interés anual del 10%, entonces esperas que al finalizar el año tengas un beneficio de 500€, y da igual que sea con interés mensual, diario o anual.
Para encontrar la fórmula que aplique a cualquier temporalidad, tan solo hay que hacer un pequeño cambio de la fórmula anterior mensual, tal que,
i_{k}=(1+i)^\frac{1}{k}-1Donde k representa el número de periodos en el que se devenga el interés.
Al hablar de meses, como hay 12 meses en un año, tendríamos que cambiarlo por 12, pero si hablamos de semestres, k=2; trimestres, k=4; días, k=365; y así sucesivamente.
Cómo calcular el interés compuesto en meses, semanas, días, trimestres, semestres, …
Una vez tienes la fórmula anterior genérica, tan solo tienes que sustituir k por el número de existen en un año con respecto a la periodicidad elegida.
En la siguiente tabla te muestro los tipos de interés compuesto en diferentes periodos para que te sirva de ejemplo y práctica.
| Anual | Semestral | Cuatrimestral | Trimestral | Mensual | Semanal | Diario |
| i | i_2 | i_3 | i_4 | i_{12} | i_{52} | i_{365} |
| 1.00% | 0.50% | 0.33% | 0.25% | 0.08% | 0.02% | 0.00% |
| 2.00% | 1.00% | 0.66% | 0.50% | 0.17% | 0.04% | 0.01% |
| 3.00% | 1.49% | 0.99% | 0.74% | 0.25% | 0.06% | 0.01% |
| 5.00% | 2.47% | 1.64% | 1.23% | 0.41% | 0.09% | 0.01% |
| 10.00% | 4.88% | 3.23% | 2.41% | 0.80% | 0.18% | 0.03% |
| 25.00% | 11.80% | 7.72% | 5.74% | 1.88% | 0.43% | 0.06% |
| 50.00% | 22.47% | 14.47% | 10.67% | 3.44% | 0.78% | 0.11% |
| 100.00% | 41.42% | 25.99% | 18.92% | 5.95% | 1.34% | 0.19% |
Estos datos también te sirven para calcular el interés anual, o cualquier periodo, siempre y cuando apliques la fórmula o la modifiques según tus datos.
Ahora imagina que tienes el interés mensual y quieres calcular el trimestral. En este caso no tienes por qué hacer dos cálculos pasando al anual y luego vuelta al trimestral, sino que lo puedes hacer directo.
Tan solo debes aplicar la ley de que buscamos que el capital final sea el mismo siempre, de este modo, (1+i_{12})^{12}=(1+i_4)^4, por lo que el interés trimestral partiendo de un interés mensual sería, i_4=\sqrt[4]{(1+i_{12})^{12}}-1.
Teniendo como ejemplo la tabla, puedes hacer todos los cambios que desees.
Diferencia entre el cálculo del interés simple y compuesto en meses
El cálculo del interés simple, es más simple, debido a que la principal diferencia es que los intereses no se reinvierten, sino que se extraen y se acumulan.
Es decir, que si inviertes 5.000€ en un año con pago mensual, cada pago que recibas te lo quedas, o te lo gastas, o haces con él lo que quieras, pero no se reinvierte.
Sin embargo, para el cálculo del interés simple mensual, se mantiene la misma filosofía, y es que bien el pago sea mensual, diario, o en cualquier periodo, el capital final o las ganancias han de ser las mismas.
Existe una particularidad, y es que el capital final a un periodo del interés simple y compuesto es el mismo y ahora entenderás por qué. Esta es la fórmula del interés simple,
C_f=C_0*(1+i*n)
Si sustituimos n=1 porque es un periodo, el resultado es el mismo. Así que ahora debemos igualar esta fórmula con la fórmula de interés mensual como hemos hecho en el caso anterior.
C_0*(1+i)=C_0*(1+i_{12}*12)Al eliminar los costes iniciales, tenemos finalmente que,
i_{12}=\frac{i}{12}Y a partir de esta expresión, podemos lograr la fórmula para interés simple a menos de un año para cualquier periodo, tan solo tenemos que hacer el mismo cambio que antes. Esta es la fórmula,
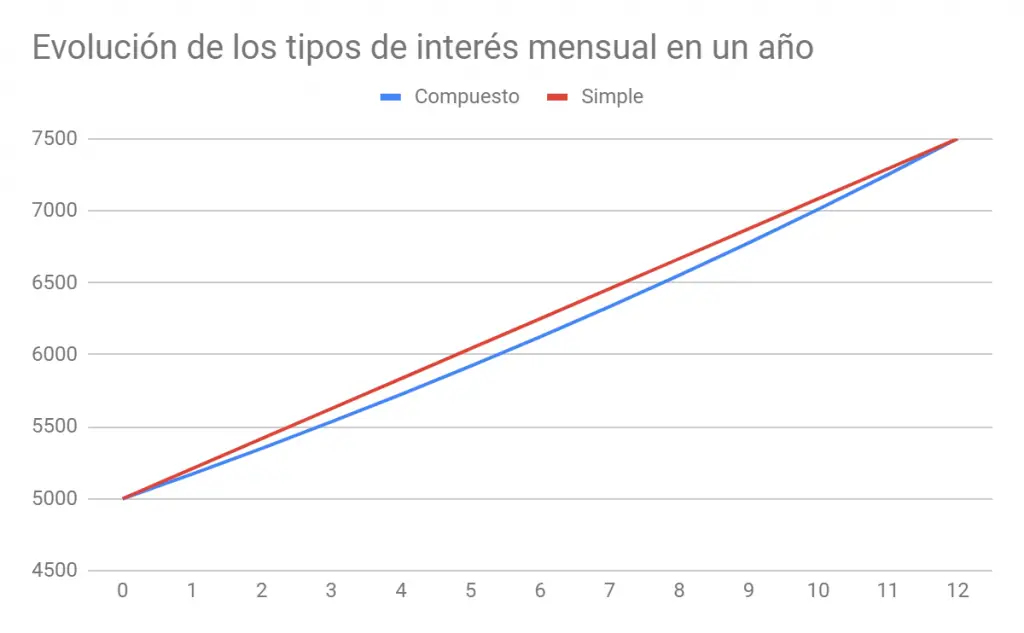
i_{k}=\frac{i}{k}En el gráfico de la izquierda se muestra que la evolución del interés compuesto frente al simple es diferente, puesto que en el simple aumenta de forma lineal, aritmética, sumatoria; mientras que el compuesto evoluciona de forma exponencial, geométrica.
Lo cierto es que, en un año, como hemos indicado antes, o más bien un periodo, el resultado es el mismo, y la diferencia se encuentra en un plazo mayor, como se puede observar en el gráfico de la derecha.
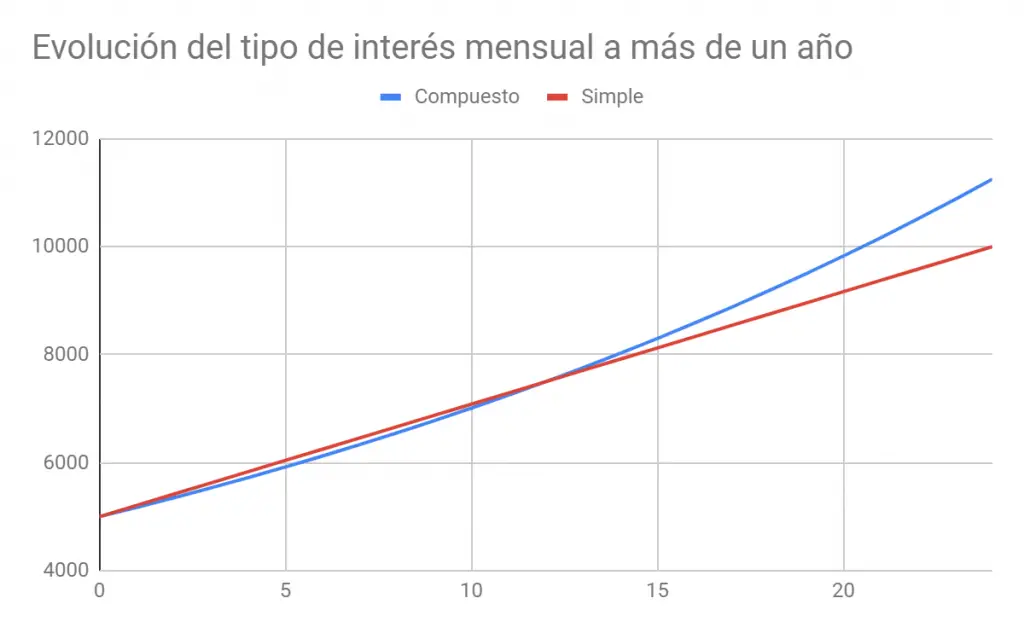
Cuanto más largo plazo, la diferencia entre el interés simple y compuesto se hace más notable.
Calcular el interés compuesto en meses, trimestres y días en Excel
Hasta ahora te he comentado cómo hacerlo, y puedes hacer los cálculos hasta con la calculadora de tu teléfono móvil. Pero quizás te interese saber cómo se hace con el ordenador.
Aunque la forma de hacerla es la misma, tan solo debes introducir la fórmula aquí explicada en la hoja de cálculo.
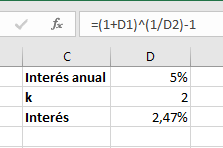
En esta imagen se observa la fórmula que se ha introducido, que es exactamente la misma que se ha descrito arriba.
El interés buscado es semestral porque k=2, pero en el caso de que se quiera buscar otro periodo, tan solo hay que cambiar el número 2.
Ocurre lo mismo que si queremos calcular otro tipo de interés, que tan solo deberemos cambiar la celda D2 del interés anual, y automáticamente se cambiará.
Como ves, es muy sencillo de hacer.
Puntos clave
El interés compuesto está presente en todos los productos financieros, además de que por simplicidad y comparación, se usa siempre el interés anual.
En cambio, en la práctica esto es diferente, porque se aplican periodos distintos de devengo, y es por ello que se hace esencial entender cómo calcular estos tipos de interés.
Hay que conocer que para realizar estos cálculos se logra sabiendo que no importa cuál sea el periodo, que al final el resultado debe ser el mismo. Partiendo de ahí, se puede calcular cualquier cambio.


Buenas ¡Muchas gracias por la explicación!
Hola buen dia. es viable calcular el interés compuesto de 01 año a un mes tan solo con dividir la tasa de interés?, es decir: 12% anual / 12 = 1% mensual ?? o tal como lo explicas se debe utilizar la formula =(1+0.12)^(1/12)-1..
Hola Eddy, es como indicas. Si solamente haces la división, estarás trabajando con interés simple. Si trabajas con interés compuesto tienes que aplicar la fórmula de la capitalización compuesta.
Saludos!!